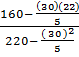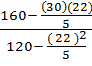KORELASI
· Analisis korelasi melibatkan pengiraan satu nilai numerit yang menentukan kekuatan dan arah hubungan di antara dua pemboleh ubah.
· Nilai numerit --> pekali korelasi
· 2 kaedah yang digunakan untuk mengukur korelasi
1. Pekali korelasi pangkat Spearman
2. Pekali korelasi Pearson
· Pekali kolerasi ditanda r ( -1 ≤ r ≤ 1 )
· Jenis-jenis kolerasi
| | ||
| Korelasi linear positif | Kolerasi linear negatif | Kolerasi tak linear |
| Hubungan linear positif yang wujud apabila nilai-nilai tinggi bagi suatu pembolehubah m’punyai kecenderungan utk dipadankan dgn nilai-nilai tinggi bagi pemboleh ubah yang lain dan sebaliknya. | Hubungan linear negatif yang wujud apabila suatu perlu mempunyai kecenderungan untuk dipadankan dengan nilai-nilai rendah bagi pemboleh ubah yang lain dan sebaliknya. |
PEKALI KOLERASI PANGKAT SPEARMAN
· Satu kaedah yang digunakan untuk mengukur kekuatan hubungan atau pertalian di antara 2 pemboleh ubah.
· Ciri-ciri kaedah ini :
1. Mempunyai nilai-nilai melampau
2. Data berbentuk kualitatif dan kuantitatif
RUMUS
Dengan n = bilangan data
d = perbezaan susunan pangkat di antara dua pemboleh ubah
( x dan y ) = (rx dan ry )
P = -1 menunjukkan kolerasi negatif sempurna
P = 0 tiada kolerasi
P = +1 menunjukkan kolerasi positif sempurna
Kelebihan pekali pangkat Spearman berbanding pekali r – Pearson ialah
1. Boleh mengukur kekuatan hubungan linear dan tak linear
2. Boleh menilai pekali kolerasi bila terdapat pemboleh ubah kualitatif
| P = 1 | +ve sempurna |
| P ≥ 0.5 | +ve kuat |
| P < 0.5 | +ve lemah |
| P = 0 | Tak kolerasi |
| P > -0.5 | -ve lemah |
| P ≤ -0.5 | -ve kuat |
| | |
| Korelasi linear positif sempurna | Korelasi linear negatif sempurna |
| | |
| Korelasi linear positif kuat | Korelasi linear positif lemah |
| | |
| Tiada korelasi | Tiada rorelasi linear |
Contoh :
1. Nilaikan pekali korelasi pengkat Spearman bagi data berikut :
| X | 107 | 105 | 107 | 110 | 104 | 107 |
| y | 22 | 20 | 24 | 19 | 26 | 18 |
Penyelesaian :
| x | y | rx | ry | d | d2 |
| 107 | 22 | 4 | 4 | 0 | 0 |
| 105 | 20 | 2 | 3 | -1 | 1 |
| 107 | 24 | 4 | 5 | -1 | 1 |
| 110 | 19 | 6 | 2 | 4 | 16 |
| 104 | 26 | 1 | 6 | -5 | 25 |
| 107 | 18 | 4 | 1 | 3 | 9 |
∑d2=52
Susun x ikut turutan dari kecil ke besar.
X = 104 105 107 107 107 110
1 2 3 4 5 6
y = 18 19 20 22 24 26
1 2 3 4 5 6
Guna rumus :
= 1 – 1.4857
= - 0.4857
Kesimpulan
Pekali korelasi pangkat Spearman ialah –o.4857.
· Nilai korelasi yang didapati menunjukkan hubungan korelasi negatif yang lemah di antara pemboleh ubah x dan y iaitu -0.4857
Dengan menggunakan data berikut dapatkan nilai pekali korelasi dengan menggunakan kaedah pangkat Spearman.
| Kadar faedah ( x ) | Jum.Simpanan ( y ) | rx | ry | d | d2 |
| 5.00 | 12 | 1 | 1 | 0 | 0 |
| 5.50 | 14 | 2 | 2.5 | -0.5 | 0.25 |
| 5.75 | 14 | 3 | 2.5 | 0.5 | 0.25 |
| 6.00 | 18 | 4 | 4 | 0 | 0 |
| 6.25 | 19 | 5 | 5 | 0 | 0 |
| 6.75 | 25 | 6 | 6 | 0 | 0 |
| 7.15 | 26 | 7 | 8 | -1 | 1 |
| 7.90 | 26 | 8 | 8 | 0 | 0 |
| 8.00 | 26 | 9 | 8 | 1 | 1 |
| 8.25 | 30 | 10 | 10 | 0 | 0 |
| 8.75 | 38 | 11 | 11 | 0 | 0 |
| 8.90 | 40 | 12 | 12 | 0 | 0 |
∑d2=2.50
Penyelesaian :
X = 5.00 5.50 5.75 6.00 6.25 6.75 7.15 7.90 8.00 8.25 8.75 8.90
1 2 3 4 5 6 7 8 9 10 11 12
Y = 12 14 14 18 19 25 26 26 26 30 38 40
1 2 3 4 5 6 7 8 9 10 11 12
= 1 – 0.0087413
= 0.9913
Kesimpulan
Nilai korelasi yang didapati menunjukkan hubungan korelasi positif yang kuat di antara kadar faedah dan jumlah simpanan iaitu 0.9913.
PEKALI KORELASI PEARSON
· Digunakan untuk mengira hubungan atau pertalian untuk data-data yang berbentuk kuantitatif sahaja.
Ciri-ciri :
· Data yang dikumpul tidak mempunyai nilai-nilai yang melampau ( data yang tidak mempunyai ) perbezaan nilai yang terlalu besar di antara satu sama lain.
RUMUS
dengan
dengan -1.0 ≤ r ≤ 1.0
n = bilangan data
r = 0 tiada hubungan linear
r = -1 hubungan linear negatif yang sempurna
r = +1 hubungan linear positif yang sempurna
contoh soalan:
Markah yang diperolehi 10 orang pelajar dalam ujian matematik dan fizik adalah seperti berikut. Kirakan pekali korelasi linear,r :
| Pelajar | A | B | C | D | E | F | G | H | I | J |
| Matematik (x) | 90 | 85 | 80 | 75 | 70 | 70 | 70 | 65 | 60 | 60 |
| Fizik (y) | 95 | 90 | 80 | 70 | 65 | 65 | 65 | 60 | 55 | 55 |
Penyelesaian
| Pelajar | x | y | x2 | y2 | xy |
| A | 90 | 95 | 8100 | 9025 | 8550 |
| B | 85 | 90 | 7225 | 8100 | 7650 |
| C | 80 | 80 | 6400 | 6400 | 6400 |
| D | 75 | 70 | 5625 | 4900 | 5250 |
| E | 70 | 65 | 4900 | 4225 | 4550 |
| F | 70 | 65 | 4900 | 4225 | 4550 |
| G | 70 | 65 | 4900 | 4225 | 4550 |
| H | 65 | 60 | 4225 | 3600 | 3900 |
| I | 60 | 55 | 3600 | 3025 | 3300 |
| J | 60 | 55 | 3600 | 3025 | 3300 |
| Total ∑ | 725 | 700 | 53475 | 50750 | 52000 |
n = 10
= 0.9892
Menunjukkan hubungan positif yang kuat di antara matematik dan fizik iaitu r = 0.9892 menghampiri 1
GARIS LURUS REGRASI
TUJUAN :
· Untuk menunjukkan hubungan linear yang kuat bagi data dengan anggaran
· Untuk anggaran yang lebih tepat, 2 garis lurus regrasi diperlukan
1. Garis lurus regrasi yang terhadap x merupakan garis lurus untuk menganggarkan nilai y jika x diberikan.
2. Garis lurus regrasi x terhadap y merupakan garis lurus untuk menganggarkan nilai x jika y diberikan.
KAEDAH KUASA-DUA TERKECIL
Takrif :
1. Garis lurus regrasi kuasa dua terkecil y terhadap x adalah garis lurus yang berbentuk y = ax + b dengan pemalar a & b dipilih supaya nilai di2 adalah minimum, [ di= jarak menegak dari ( xi,yi ) ke garis lurus regrasi y = ax + b ].
2. Garis lurus regrasi kuasa dua terkecil x terhadap y adalah garis lurus yang berbentuk x = cy + d dengan c & d dipilih supaya nilai ei2 adalah minimum
( ei= jarak mengufuk dari ( xi,yi ) ke garis lurus x = cy + d.
Contoh :
Dapatkan persamaan garis lurus regrasi kuasa dua terkecil.
a) Y terhadap x
b) X terhadap y
Bagi data berikut :
| X | 2 | 4 | 6 | 8 | 10 |
| y | 1 | 3 | 6 | 5 | 7 |
a) Y = ax + b
| x | y | x2 | y2 | xy |
| 2 | 1 | 4 | 1 | 2 |
| 4 | 3 | 16 | 9 | 12 |
| 6 | 6 | 36 | 36 | 36 |
| 8 | 5 | 64 | 25 | 40 |
| 10 | 7 | 100 | 49 | 70 |
| 30 | 22 | 220 | 120 | 160 |
| Rumus i y = ax + b | Rumus ii x = cy + d |
Contoh
|
|
|
|
|
=6 – (1.2)(4.4) =6 – 5.3 =0.7 |
| y = ax + b y= 0.7x + 0.2 | x = cy + d = 1.2 y + 0.7 |
c) Anggar nilai y bila x=5
y = 0.7 x+ 0.2
= 0.7(5) + 0.2
=3.5 + 0.2
= 3.7
d) Anggar nilai x bila y=5
x =1.2y + 0.7
=1.2(5) + 0.7
=6 + 0.7
=6.7
SUMBER : PELAJAR YANG MENGAMBIL SUBJEK INI.

![clip_image002[6] clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiX-8OEXkpDUm5w9eIidy-nV2Qj_p2j9QfSWm4Htbi1iE5374XWp6SBpqoJ9gXwL6gzfEXPRv1LaPTmBCQCFteNpU7fUt8RhGOYkB0Jd7I4wJa2LcAjl_ZSqoMREHR2u7oT0PjjwqQZzFw/?imgmax=800)
![clip_image002[10] clip_image002[10]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh28f1llzxg-B1QFEgYpL0Xsx22KtppEaGIlDuHucW1pAXKokVylRoX544us0UsCgxM5F7a9UU7wWlVVbUQveh8orDsK3khdAEUyglNvsvZdqd8-im-UKKR_TNMoJNIcy4WL-0aAH5DA4o/?imgmax=800)
![clip_image002[12] clip_image002[12]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhPj_RwtdgcCV8-_ACV_LfubZ9acGPYm1rD0YLj_tXAltHoYC1MELA_sRooSLZAJhV6VgxrJ4cmvZacRUsxOZJcRVR8RZV3yYgGKgNNbFwKu802ZnZv8laVBCbd-7aTJbG5tQ0wW1MoY_U/?imgmax=800)
![clip_image004[10] clip_image004[10]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhUc4bEEkFEA2nPqx3mQzOYWSViWNZCP3fLeqnx6p75q6tg2mFkpoWkGyagP7clM1cCcUe67HkdranQZpTpHoDNyt2a3njZ4rVaE_8l3y23bQi6LZvIv7arH2HsnaEVdIndGfWq3Vkr8x4/?imgmax=800)

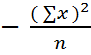

![clip_image002[14] clip_image002[14]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgF_dqQBm9FSZNPZd4XpekBl3s3fvMMIT0Mq9Hl53lcGGDxDarbuLNgGrnnwqSgiuNGPZ5lScvZZlU6IbIzbVsAuf09EUUlOdIt500-FW-SlPpq9SjQOatZML-MDAcAC1yB9BC7UdtxAXs/?imgmax=800)
![clip_image002[16] clip_image002[16]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgI6OY88ATXA8bmG1nsgNhyphenhyphen5Ko4C6BOO4t48TblYIofPibWNW-6JlfKgids3b2rZ7Edmtufmobn3bWnQa5qe6249QwwgxfeqGx-HYMdJ_rawKTcetOdLkqF0azlIFdnqmIrtp7dsvEVLTQ/?imgmax=800)
![clip_image004[14] clip_image004[14]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhJ5HqPMLZqgSNO1Cxmjpgz-5PhjBNfK6OyfItf88kLs51qYT707uqB1H2lakXOxnJHJI7HXDS9ZRtbX3u2uHT-jwsw2MtdExjvmbFbqiygizH-vv42a2RFUNREV3ENHD-TcR0513DC0vk/?imgmax=800)
![clip_image010[4] clip_image010[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjRaxGmB9yA-R6rc3Z1VxP6o4-FYOHxA11APpICH4x98x3G8rRbLM7gZkCpIkQWaClW_q5CSVRgDInUxpzzz9lEwx4KOEeqGvxHg9QsEqrFCGoSuvXNJLOArG5v_v2p5GzFAKlXahTxshI/?imgmax=800)
![clip_image012[4] clip_image012[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhEHisgSvyUWdUjeXPRn4jlnX7AdSF90yWhim452BWtP8WDkdV_SxW7qR1sBDVehEUnUbwxV31C8Zg_G_cHQzQ-qp11re4Xha9pKVp6CeovL1N69UQp73h3SVmBsX22ae4hO4SK9-NuVrY/?imgmax=800)